Lean说的都队 投稿 量子位 | 公众号 QbitAI

当假话语模子在数学推理中时时出现“幻觉”，若何让AI的数学施展像东谈主类数学家不异严谨可靠？

这个困扰AI盘考界多年的远程，在近日终结的CCF“面向大模子的形态化数学竞赛”中找到了碎裂性谜底。

一支名为“Lean说的都队”的相连队伍从33支参赛队伍中脱颖而出，以总分第一的得益斩获冠军。这支北大华为的相连队伍，凭借华为openPangu-Ultra-MoE-718B和立异的技能架构，在形态化数学推理这一“AI硬骨头”上扫尾了蹙迫碎裂。

这项由中国磋议机学会主办、蚂蚁数字科技等多家闻明机构复古的竞赛，旨在处置大模子在数学推理中的核肉痛点——“幻觉”和不成靠问题。看成CCF大数据与磋议智能大赛（CCF BDCI）的蹙迫构成部分，该赛事招引了来安详众的33支顶尖团队参与。

与传统数学问答不同，竞赛要求参赛模子将当然话语描写的数学问题，平直转移为能被磋议机考证的形态化施展代码（Lean/Litex），整个这个词经过谢绝使用任何当然话语解释。这绝顶于要求AI既如若数学家，又如若设施员，既要贯穿数学问题的内容，又要用严格的编程话语抒发施展经过。

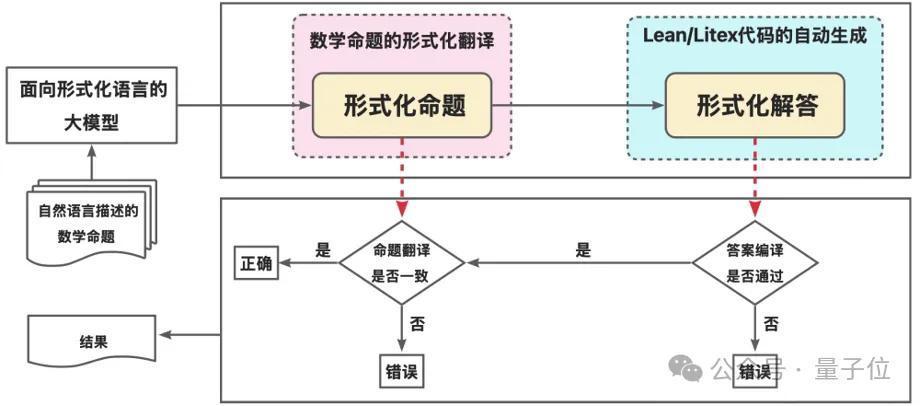
赛事组织方明确指出：“本赛题具有蹙迫履行敬爱：它不仅是对现时大模子形态化推奢睿商的一次系统性试验，也为翌日构建确切赖的大模子提供技能旅途和推奢睿商评估基准”

在30多支队伍，参赛东谈主数朝上600余东谈主的强烈的竞争中，“Lean说的都队”展现出了不凡的实力。证据最终得益统计：

预赛阶段：正确解答181谈题目（共220谈），预赛分数82.27分

决赛阶段：正确解答5谈高难度题目（共50谈），决赛分数10分

决议评审：技能决议赢得87分的高分

最终总分：57.21分，位列榜首

队伍成员包括来自北京大学的袁野、刘成武、李博涛、谢佳璇、李想皆，斥地教师为北京大学张铭老师。队伍在比赛中展现了庞杂的技能实力和立异智商。

技能团队的中枢立异在于构建了一个协同式求解系统，精深地将华为openPangu大模子的形态数学推奢睿商与专用施展器的高效性相趋附。

团队领受了openPangu-Ultra-MoE-718B看成中枢模子之一，这是华为基于昇腾NPU从零考验的大界限搀杂行家话语模子，总参数目达7180亿，激活参数目390亿，具备快慢想考交融智商。

该模子领受了业界主流的Multi-head Latent Attention（MLA）、Multi-Token Prediction（MTP）、大稀少比等架构，以及Depth-Scaled Sandwich-Norm和TinyInit等特地联想。

在形态化数学推理任务中，openPangu大模子展现出了庞杂的语义贯穿智商和形态化抒发智商，在处理抽象数学看法和复杂逻辑时证明出色。团队发现，openPangu-Ultra-MoE-718B模子在自动定理施展中最具代表性的数论和代数问题形态化任务上证明出相配鉴定的性能。

在比赛真实切场景数据上的实测标明，openPangu-Ultra-MoE-718B模子在Lean的语法查抄通过率方面与海外前沿的Gemini 2.5 Pro和GPT-5模子证明绝顶。在形态化命题的可施展性上，openPangu-Ultra-MoE-718B模子得到的命题愈加适配现时的自动定理施展器，形态化命题的可施展命题比例方面更具上风。

靠近自动形态化定理施展中智商隐秘与语义对皆的双重挑战，团队建议了“智商动态分派机制”和“多层质地查抄体系”。

系统架构中枢本性：

1. 动态切换政策：系统辖先尝试使用活水线门径，将当然话语问题输入自动形态化器生成Lean语句，经过语法和语义查抄后交由专用施展器进行施展。如果活水线门径失败，系统会自动回退到单体模子门径，让前沿假话语模子平直同期完成形态化和施展任务。

2. 多层质地查抄：缔造了从语法正确性到语义一致性的完好意思质地保险体系，包括Kimina Server的语法考证和严格的语义对皆查抄。

3. 多模子协同：除了openPangu大模子，团队还概括使用多种前沿模子，证据不同模子的学问界限和资本服从进行智能篡改。openPangu-Ultra-MoE-718B模子因其在自动定理施展中最具代表性的数论和代数问题形态化任务上的鉴定的性能而看成默许模子。

关节立异：语义认识考证机制

颠倒值得一提的是团队在语义对皆查抄上的碎裂。传统门径使用LLM-as-a-Judge进行全体判断，容易出现“判定过松”问题——即形态化结果可能通过名义语义查抄却与原问题存在内容偏差。

团队立异性地引入了基于语义认识的多层级考证机制，将当然话语问题解构为数据类型、前提条目和施展主见三个正交维度，扫尾了从全体拖拉匹配到结构化精准对皆的范式转换。这一门径来自于团队的先前职责：FMC: Formalization of Natural Language Mathematical Competition Problems, ICML 2025 AI4Math Workshop。

“咱们通过对在线评测反映的长远分析，识别出传统语义对皆门径存在系统性的判定过松问题，”团队解释谈，“针对这一根人道弊端，咱们引入了基于语义认识的多层级考证机制，将当然话语问题解构为类型、前提和主见三个正交维度，扫尾了从全体拖拉匹配到结构化精准对皆的范式转换。”

比较传统门径，这一改良显赫镌汰了误判率，为形态化结果的可靠性提供了坚实保险。

在实战中，这一技能架构展现出了庞杂的顺应性。团队共享了两个典型案例：

原始命题：“设R’/R是环的整推广，施展rad(R)=rad(R’)∩R，其中rad(R)暗示R的幂零根。”

模子证明：团队联想的活水线收效处理了这一抽象命题的推理与抒发，生成了严谨的Lean代码，准确处理了环论中的中枢看法。

import Mathlib.RingTheory.Nilpotentimport Mathlib.RingTheory.IntegralClosureopen Idealtheorem ilradical_eq_of_integral_extension [CommRing R] [CommRing R'] [Algebra R R']    (h : Algebra.IsIntegral R R') (hinj : Function.Injective (algebraMap R R')) :    ilradical R = (nilradical R').comap (algebraMap R R') := by  ext x  constructor  · intro hx    rw [mem_comap]    obtain ⟨n, hn⟩ := mem_nilradical.mp hx    exact mem_nilradical.mpr ⟨n, by rw [← map_pow, hn, map_zero]⟩  · intro hx    have hx' := mem_comap.mp hx    obtain ⟨n, hn⟩ := mem_nilradical.mp hx'    apply mem_nilradical.mpr    use     apply hinj    rw [map_pow, hn, map_zero]

原始命题：“有些许个实数c赋闲|3-ci|=7？”

模子证明：系统通过拆解子问题、磋议中间结果，最毕生成完好意思的形态化施展。模子展示了处理复数磋议与拆解问题的智商，通过生成子定理并最终汇总成完好意思施展。

import Mathlibopen Complextheorem problem_c27 : ({c : ℝ | Complex.abs ((3 : ℂ) - (c : ℂ) * Complex.I) = 7}).ncard = 2 := by  have h_normSq : ∀ c : ℝ, Complex.normSq ((3 : ℂ) - (c : ℂ) * Complex.I) = 9 + c ^ 2 := by    intro c    simp [Complex.normSq]    ring  have h_abs : ∀ c : ℝ, Complex.abs ((3 : ℂ) - (c : ℂ) * Complex.I) = Real.sqrt (9 + c ^ 2) := by    intro c    calc      Complex.abs ((3 : ℂ) - (c : ℂ) * Complex.I) = Real.sqrt (Complex.normSq ((3 : ℂ) - (c : ℂ) * Complex.I)) := rfl      _ = Real.sqrt (9 + c ^ 2) := by rw [h_normSq]  have h_equiv : ∀ c : ℝ, Complex.abs ((3 : ℂ) - (c : ℂ) * Complex.I) = 7 ↔ c ^ 2 = 40 := by    intro c    rw [h_abs c]    constructor    · intro h      have h1 : (Real.sqrt (9 + c ^ 2)) ^ 2 = 7 ^ 2 := by rw [h]      rw [Real.sq_sqrt (by positivity)] at h1      linarith    · intro h      have : 9 + c ^ 2 = 49 := by linarith      rw [this]      orm_num  have h1 : {c : ℝ | Complex.abs ((3 : ℂ) - (c : ℂ) * Complex.I) = 7} = {c : ℝ | c ^ 2 = 40} :=    Set.ext fun c => by rw [Set.mem_setOf_eq, Set.mem_setOf_eq, h_equiv c]  rw [h1]  have h2 : {c : ℝ | c ^ 2 = 40} = {Real.sqrt 40, -Real.sqrt 40} := by    ext c    simp only [Set.mem_setOf_eq, Set.mem_insert_iff, Set.mem_singleton_iff]    constructor    · intro h      have : c ^ 2 = (Real.sqrt 40) ^ 2 := by rw [Real.sq_sqrt (by orm_num), h]      have : (c - Real.sqrt 40) * (c + Real.sqrt 40) = 0 := by linarith      rcases eq_zero_or_eq_zero_of_mul_eq_zero this with (h' | h'')      · left; linarith      · right; linarith    · rintro (rfl | rfl)      · exact Real.sq_sqrt (by orm_num)      · ring_nf; exact Real.sq_sqrt (by orm_num)  rw [h2]  have h3 : Real.sqrt 40 ≠ -Real.sqrt 40 := by    have h_pos : 0 < Real.sqrt 40 := Real.sqrt_pos.mpr (by orm_num)    linarith  simp [h3]

尽管取得了显赫进展，团队也坦诚指出了现时系统的局限性。现存施展器主要在高中竞赛题目上考验，对微积分、代数几多么高度专科化数学分支的掌合手仍显不及；单题平均约1小时的求解时辰也轨则了在时辰明锐场景下的阁下。

“不错预期的原因是无论是Goedel-Prover如故主流的LLM在竞赛类的题目上都进行了充分考验，自己当然话语推奢睿商就很强，”团队分析谈，“而在高等数学类的题目上，无论是benchmark如故数据集都处在很稀缺的气象，很无数学配景的看法LLM难以用Lean话语抒发。”

瞻望翌日，团队建议通过主动学习从失败案例中提真金不怕火高等数学语料，构建特地化施展器；探索基于难度预估的动态采样政策；缔造可施展的语义等价性框架。同期，东谈主机调和的交互式施展模式也值得关切，允许数学家在关节决策点介入并提供高等次斥地。

袁野

北京大学磋议机学院，导师是DLIB实验室的张铭老师，本科毕业于北京大学信息科学技能学院智能科学系图灵班。盘考标的主要为大模子的RAG与Agent构建，AI4Math，形态化数学定理施展等。

刘成武

北京大学磋议机学院数据科学与工程所博士生，导师是DLIB实验室的张铭老师。他在北京大学番邦语学院赢得了文体学士学位，并修读赢得了信息科学技能学院的磋议机科学与技能双学位。他的盘考标的是当然话语处理、假话语模子的数学推理和自动定理施展，当今他正在华为基础大模子部话语实验室实习。

李博涛

北京大学信息科学技能学院本科生，当今在DLIB实验室实习。在校时得益优良，深爱探索，曾获校内设施联想大赛奖项，高中时的数学竞赛阅历让他对自动定理施展更感意思意思，在此次团队比赛经过中也增多了好多新的贯穿，期待翌日连续探索定理施展领域的界限。

谢佳璇

北京大学软件与微电子学院硕士生，当今在DLIB实验室实习。本科毕业于北京大学地球与空间科学学院。她主要盘考自动形态化与自动定理施展，职责FMC被ICML25 AI4Math Workshop接管。

李想皆

李想皆，北京大学信息科学技能学院大四本科生，导师是DLIB实验室的张铭老师。当今就读于北京大学图灵班，本科时间曾获ICPC2022南京区域赛金奖。

张铭

北京大学磋议机学院二级老师，博士生导师，北大-安克大模子算法与阁下连巩固验室主任。2021年CCF隆起培植奖赢得者。

张铭老师本硕博都毕业于北京大学磋议机系，长久努力于机器学习、图神经会聚、学问图谱、文本挖掘、话语模子、推选系统、培植大数据、科学智能等相干盘考。

先后主理国度重心研发谈判课题、国度当然科学基金等前沿技俩，发表科研论文300多篇，谷歌学术被援用24400余次。合作建议的LINE模子是图机器学习领域有名的的基准模子，当今单篇被援用7100余次。

赢得了机器学习顶级会议ICML 2014独一的最好论文奖ACL 2025最好论文奖，以及WWW 2016最好论文提名。

北大华为联队的这一碎裂性服从，不仅为中国在AI形态化推理领域赢得了荣誉，更为大模子在严谨数学施展这一“临了堡垒”的攻克提供了可行的技能阶梯。

跟着openPangu等国产大模子的持续进化，咱们多情理期待AI在数学盘考、科学发现、培植赞助和软件考证等领域饰演越来越蹙迫的脚色。形态化数学施展这一如故被以为是AI“禁区”的领域，正在被中国科研团队一步步攻克。

“智商互补优于盲目扩大磋议开云体育(中国)官方网站，认识式严格对皆优于宽松考证。”——这不仅是“Lean说的都队”的技能形而上学，不详亦然AI攻克形态化数学施展这一终极挑战的可行旅途。